The idea has been floating around that the scaling of pre-training is hitting a soft wall, and scaling inference-time compute is now the new thing. Why so? Why this shift in scaling paradigm? Why is scaling pre-training no longer effective? In this post, I try to share a technical perspective, drawing from my past experience in scaling law research.

The common wisdom of LLM scaling law is that some “loss” $L$ decreases as a function of the amount of pre-training compute $C$:

\[L(C) = \frac{A}{C^\alpha} + E\]

where $A, \alpha, E$ are scalar parameters specific to the definition of loss and the model family. Normally, $L$ is defined the language modeling loss on some held-out eval set, but a few papers (including ours) shows that $L$ can also be a loss on some “downstream task” (e.g., the LM loss on the answer tokens in a QA task). This functional form is highly empirical and found to work well by the Chinchilla paper and others, so we base our further discussion assuming that this is a good model of how loss terms scale.

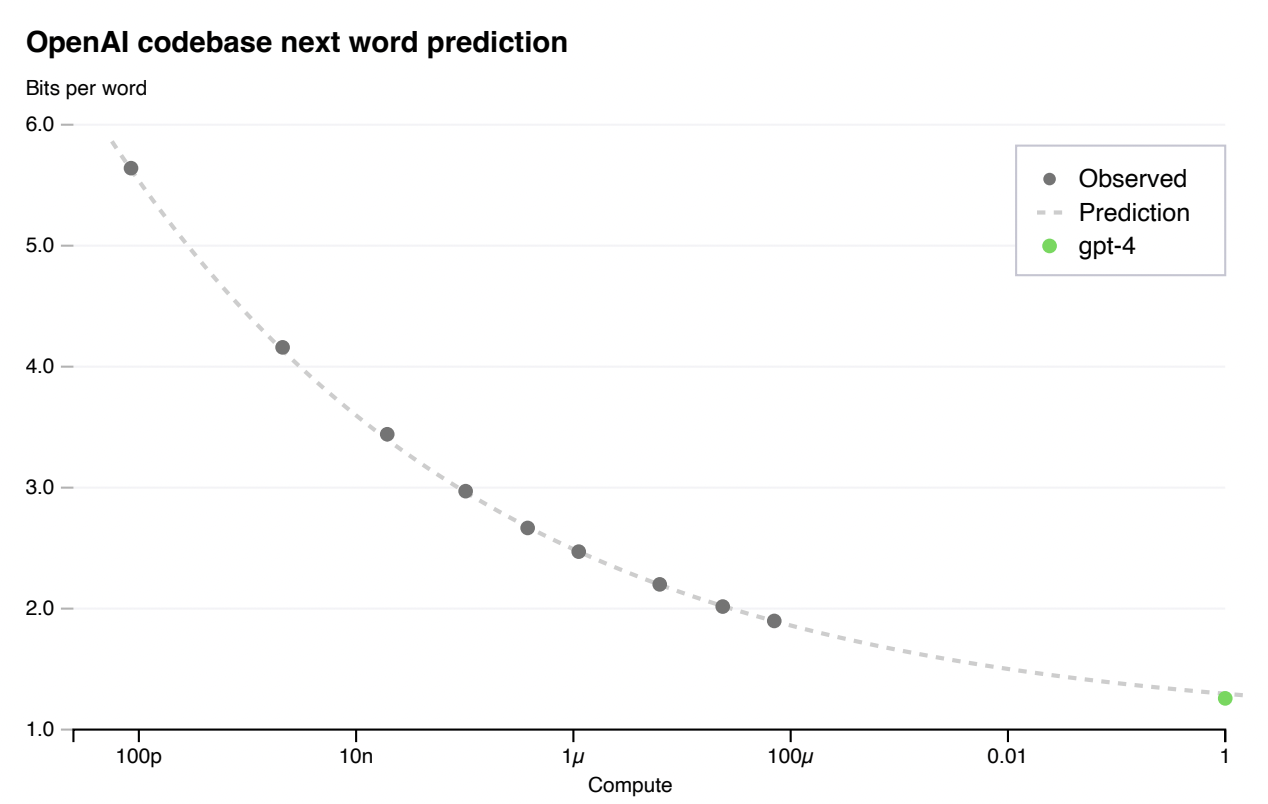Scaling of loss term A typical scaling chart of task loss vs compute, taken from the GPT-4 technical report.

The above equation characterizes the “loss” terms. If we want to figure out how the accuracy on downstream task scales with compute, we can map the loss (on that downstream task) to the task accuracy. Within the same family of models, this mapping is usually quite clean (i.e., loss is quite predictive of accuracy). However, the mapping is not linear: it often takes a “sigmoidal” shape, with accuracy being steadily low when loss is high, grows rapidly in a certain range of loss, and finally saturating and plateauing when loss further decreases.

This non-linear mapping between loss and accuracy is, to some extent, the source of the seemingly “emergent” behavior of LLMs on tasks. Loss scales rather smoothly as model and data scale, but there’s a rough point of scale at which the accuracy suddenly grows beyond triviality. If we model this mapping with a sigmoidal function $Acc(L) = 1 / (1 + e^{k (L - L_0)})$, we call the centroid of the rapidly-growing region $L_0$ the “inflection point”.

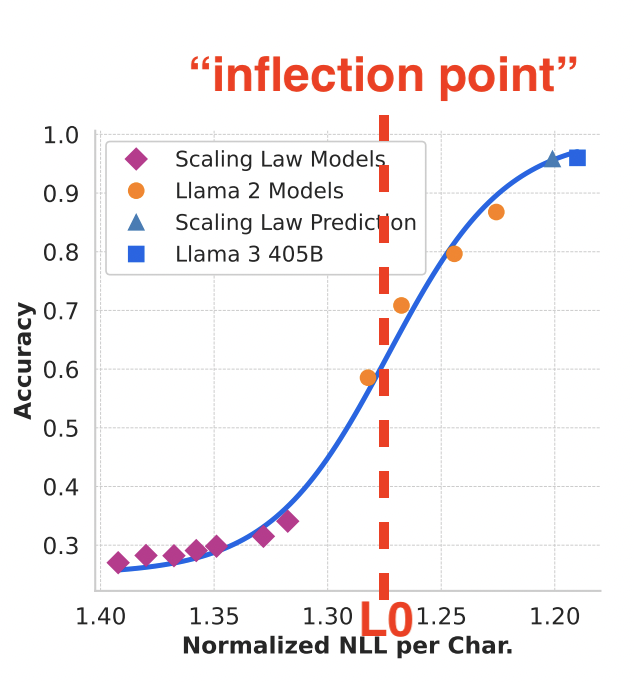Illustration of loss-accuracy mapping A typical task loss-accuracy mapping, adapted from the Llama-3 paper. The mapping takes a sigmoidal shape, with an “inflection point” near which accuracy grows rapidly.

Now, if it happens that $L_0 « E$ for a task, the inflection point is beyond reach of any scale of compute, and scaling won’t bring us any real progress on that task. Fortunately, for all tasks that I have worked with (in the context of scaling law research), we found $L_0 » E$, and thus it is possible to make a lot of progress via scaling. There may be something deep and profound in there, but that is beyond the scope of this post.

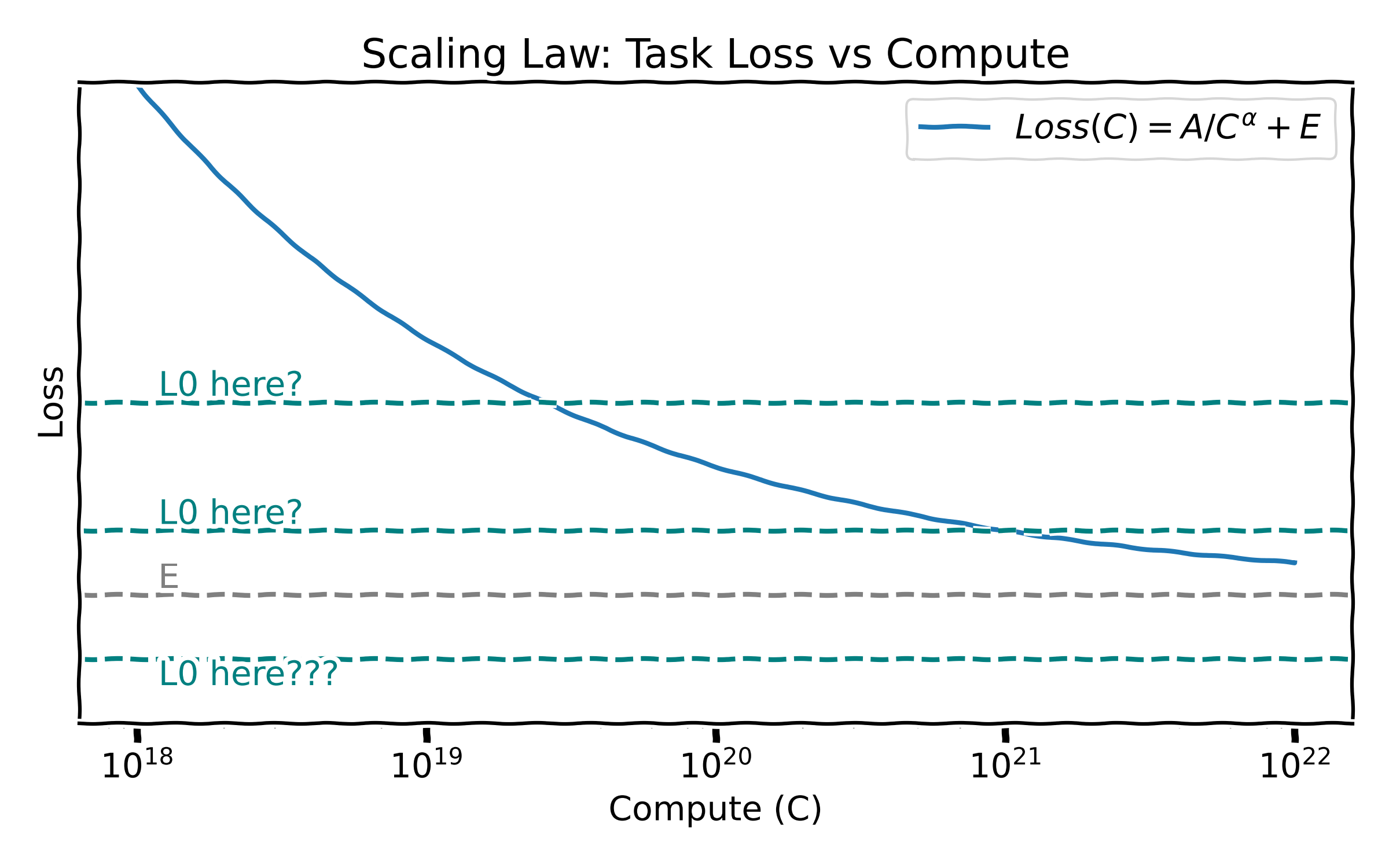Make a plot that depicts the scaling law of task loss vs compute: $Loss(C) = A/C^\alpha + E$. Draw a horizontal dashed line for the value of E (the irreducible loss) and add text "E" next to the line. Using another color, draw two more dashed lines, one above E and one below E, and add text "L0 here?" next to each of these lines. Plot in xkcd style. Where is the inflection point $L_0$ compared to the asymptotic limit $E$? (Plotting script generated by o3, prompt in the alt text)

For sake of this discussion, let’s assume we have $L_0 » E$. Then the problem is if such scaling is economically efficient, and how fast such scaling can be made. We know from Moore’s Law that with a fixed cost, the amount of compute you get roughly grows exponentially over time. (Of course, you can throw more $$$ into the project, but this has a lower ceiling because you have a capped budget, and empirically this can grow no faster than exponential due to the engineering work needed to scale up.) This growth is characterized by differential equation

\[\frac{dC}{dt} = k \cdot C\]

where $k$ is a constant.

Exponential growth sounds pretty nice, huh? Well, now let’s look at how the loss term improves over time, by applying the chain rule:

\[\frac{dL}{dt} = \frac{\partial L}{\partial C} \cdot \frac{dC}{dt} = \big( A \cdot (-\alpha) \cdot C^{-(\alpha + 1)} \big) \cdot (k \cdot C) = -A \alpha k \cdot C^{-\alpha}\]

$A, \alpha, k$ are all constant terms, so this means this rate is proportional to $C^{-\alpha}$, which shrinks exponentially over time!

Furthermore, the total amount of loss reduction over an infinite amount of time is actually bounded. This can be seen by taking the integral:

\[C = b \cdot e^{k \cdot t} \\ \frac{dL}{dt} = -A \alpha k b \cdot e^{\alpha k \cdot t} \\ \int_{t=0}^{+\infty}{\frac{dL}{dt}} = -Ab\]

This means there’s a chance that no matter how long you keep pushing the scaling of training compute, you never reach the inflection point and thus never make meaningful progress on that task.

These two reasons – the exponential slowdown of progress and boundedness of reducible loss via scaling – explain why we need to find new scaling paradigms. It may be scaling test-time compute. It may be scaling up RL training. But yeah, we are indeed hitting a soft wall of scaling pre-training, and as computer scientists, when one scaling paradigm is depleted, we always seek for new ways of scaling that gives higher marginal return.